

I think it's doesn't need to be that complicated. Hi, mikemcgarry's is good but it uses similar triangles to prove. Please let me know if you have any questions on what I've said here. Here's another geometry DS, a little closer to the actual level of difficulty of the GMAT itself. Therefore, Statement #2 is insufficient.ĭoes all this (including everything in the pdf) make sense? If we know the altitude and not the base, that's not enough. Statement #2: Line AH, the altitude of parallelogram ABCD, is 5.Īrea of a parallelogram = (base)*(altitude). Leaving those details aside for the moment, Statement #1 is sufficient.
Picture of parallelogram pdf#
Why do the rectangle and parallelogram have equal area? You will see the complete geometric argument in the pdf attachment to this post. Well, to cut to the chase, this statement is sufficient because the rectangle and the parallelogram must have equal area. Statement #1: The area of rectangle DEFG is 8√5. Area of a parallelogram exampleĪ parallelogram has sides 35 cm and 17 cm, with a height of 11 cm.As a geometry geek myself, I found this a very cool geometry problem, but I will say - it is WAY harder than anything you would be expected to figure out for yourself on the real GMAT. The area of a rectangle is easy, remember? Length x width in square units, which is the same as base x height (b x h) in square units. Move that cut off triangle over to the right side and the parallelogram is suddenly a rectangle. That means, no matter the angles we push and pull the parallelogram into, the four sides enclose the same area.Īnother way to think of it is to consider cutting off a triangle from, say, the left side of the parallelogram to leave a nice, perpendicular corner. At some point, we can make every interior angle a right angle and get a rectangle. That calculation seems too simple and does not seem to take into account the angled sides, does it?īut consider, we can move the parallelogram and change its angles.
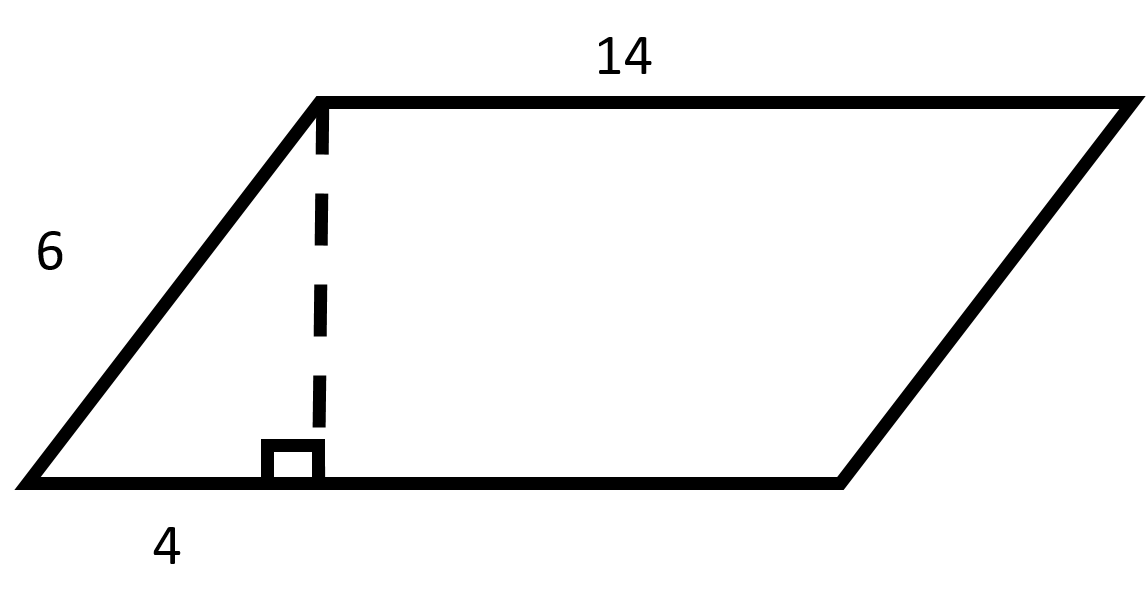
Picture of parallelogram how to#
If you know the length of base b, and you know the height or width h, you can now multiply those two numbers to get area using this formula:Ī r e a = 162 i n 2 area=162i a re a = 162 i n 2 How to calculate the area of a parallelogram We need to find the width (or height) h of the parallelogram that is, the distance of a perpendicular line drawn from base CD to AB. The width (or height) of the crate – the distance straight across from the base to the other side – could vary depending on the inside angles of vertices A, B, C and D. The two short sides, at 12 inches, are BC and DA. Side CD forms the base ( b) of our parallelogram. The two long sides, at 18 inches, are AB and CD. The four vertices (corners) are A, B, C and D. We can name the various parts of our orange-crate parallelogram. Think of our wobbly orange crate we could nearly collapse it flat, but its two short sides would always be 12 inches.
This is where things get tricky, because the distance along either short side is not necessarily its width. The length of any linear geometric shape is the longer of its two measurements the longer side is its base.įor any parallelogram, we need to know the length of a longer side (base), and its width. Finding the area of a rectangle, for example, is easy: length x width, or base x height. If you noticed the three special parallelograms in the list above, you already have a sense of how to find area. Its sides never change their length, but the crate's height (or width) changes. If you push or pull the crate so it leans more or less, every shape it takes is a parallelogram. If you turn the crate so one of its 18-inch sides is flat on a table, the crate naturally leans (because it had no bottom to hold the four sides rigid). Two of the crate's sides are 12 inches and the other two are 18 inches. Suppose you built a crate to hold, say, oranges, but you forget to put a bottom on it. Three quadrilaterals, a rhombus, a square, and a rectangle are specific types of parallelograms.


 0 kommentar(er)
0 kommentar(er)
